竖直放置的一对平行金属板的左极板上，用长为L的轻质绝缘细线悬挂一个带电量为q质量为 m的小球，将平行金属板按如图所示的电路图连接。当滑动变阻器R在a位置时，绝缘线与左极板的夹角为θ1=30°，当将滑片缓慢地移动到b位置时，夹角为θ2=60°。两板间的距离大于L，重力加速度为g。
（1）求小球在上述两个平衡位置时，平行金属板上所带电荷量之比Q1︰Q2；
（2）若保持变阻器滑片位置在a处不变，对小球再施加一个拉力，使绝缘线与竖直方向的夹角从θ1=30°缓慢地增大到θ2=60°，求此过程中拉力做的功W。
如图所示的匀强电场中，有a、b、c三点，ab＝5cm，bc＝12cm，其中ab沿电场方向，bc和电场方向成60°角，一个电量为q＝4×10－8C的正电荷从a移到b电场力做功为W1＝1.2×10－7J，求：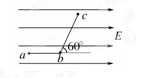
(1) a、b两点的电势差Uab
(2) 匀强电场的电场强度E
(3) 电荷从b移到c，电场力做的功W2.
场源电荷Q＝2×10－4 C，是正点电荷．检验电荷q＝－2×10－6C，是负点电荷，它们相距r＝1 m，且都在真空中，如图所示．（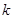
=9.0×l09 N．m2/C2）求：
(1)q受的静电力．
(2)q所在的B点的场强EB.
(9分)如图所示，在绝缘水平面上，相距为L的A、B两点处分别固定着两个等量正电荷。a、b是AB连线上两点，其中Aa=Bb=L/4，a、b两点电势相等，O为AB连线的中点。一质量为m带电量为+q的小滑块（可视为质点）以初动能E0从a点出发，沿AB直线向b运动，其中小滑块第一次经过O点时的动能为初动能的n倍（n>1），到达b点时动能恰好为零，小滑块最终停在O点，求：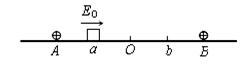
（1）小滑块与水平面间的动摩擦因数μ；
（2）Ob两点间的电势差Uob；
（3）小滑块运动的总路程s。
如右图所示电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm．电源电动势E="24" V，内电阻r="1Ω" ，电阻R="15Ω" ．闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间．若小球带电荷量为q=1×10-2C,质量为m=2×10-2kg，不考虑空气阻力（取g=10m/s2），小球恰能到达A板，求：
（1）电容器两板间的电压；
（2）滑动变阻器接入电路的阻值；
（3）电源的输出功率。
(8分)如图所示，电阻R1＝12Ω，R2＝8Ω，当开关S断开时，电流表A的示数为0．5A；当S闭合时，A的示数为0.75A。试求：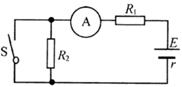
（1）电源的电动势和内电阻分别是多少?
（2）S闭合时，电源的效率多大？