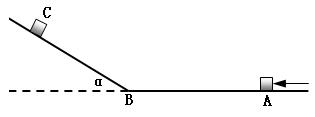
如图所示，AB为水平轨道，A、B间距离s=2m，BC是半径为R=0.40m的竖直半圆形光滑轨道，B为两轨道的连接点，C为轨道的最高点。一小物块以v0=6m/s的初速度从A点出发，经过B点滑上半圆形光滑轨道，恰能经过轨道的最高点，之后落回到水平轨道AB上的D点处。g取10m/s2，求：
（1）落点D到B点间的距离；
（2）小物块经过B点时的速度大小；
（3）小物块与水平轨道AB间的动摩擦因数。
如图所示，一根不可伸长的轻绳两端各系一个小球a和
b，跨在两根固定在离地高度为H的光滑水平细杆A、B上，质量为m的b球与B的距离为L，质量为4m的a球放置于地面上。把b球从水平位置由静止释放，求：
（1）a球
对地面的最小压力
为多大？
（2）已知细线能承受的最大拉力Fm=4mg，现给b球竖直向下的初速度，当b球运动到B点的正下方时细线恰被拉断，求b球落地点与B点的水平距离。
物体A的质量m1="1" kg，静止在光滑水平面上的木板B的质量为m2="0.5" kg、长L=1m，某时刻A以v0="4" m/s的初速度滑上木板B的上表面，为使A不致于从B上滑落，在A滑上B的同时，给B施加一个水平向右的拉力F，若A与B之间的动摩擦因数µ=0.2，试求拉力F应满足的条件．(忽略物体A的大小，取g="10" m/s2)
如图甲所示．竖直平面内的光滑轨道由直轨道AB和圆轨道BC组成，小球从轨道AB上高H处的某点静止滑下，用力传感器测出小球经过圆轨道最高点C时对轨道的压力为F，并得到如图乙所示的压力F随高度H的变化关系图象．（小球在轨道连接处无机械能损失，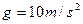
）求：
（1）小球的质量和圆轨道的半径。
（2）试在图乙中画出小球在圆轨道最低点B时对轨道的压力F随H的变化图象。
长为L的平行金属板水平放置，两极板带等量的异种电荷，板间形成匀强电场，一个带电为＋q、质量为m的带电粒子，以初速v0紧贴上板垂直于电场线方向进入该电场，刚好从下板边缘射出，射出时末速度恰与下板成30o角，如图所示，不计粒子重力，求：
（1）粒子末速度的大小。
（2）匀强电场的场强。
（3）两板间的距离。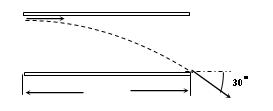
如图所示，在水平面AB上，水平恒力F推动质量为m=1kg的物体从A点由静止开始做匀加速直线运动，物体到达B点时撤去F，接着又冲上光滑斜面（设经过B点前后速度大小不变），最高能到达C点。用速度传感器测量物体的瞬时速度，并在表格中记录了部分数据。已知物体和水平面间的动摩擦因数μ=0.2。求：（g=10m/s2）
| t/s |
0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
| v/m•s-1 |
0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
(1) 恒力F的大小。
（2）斜面的倾角α。