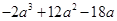李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
| 测试成绩 |
 |
 |
 |
 |
 |
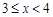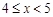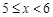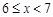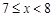合计 |
| 频数 |
3 |
27 |
9 |
m |
1 |
n |
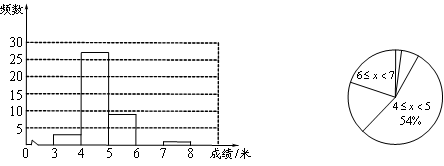
请你结合图表中所提供的信息，回答下列问题：
（1）表中m= ，n= ；
（2）请补全频数分布直方图；
（3）在扇形统计图中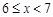，这一组所占圆心角的度数为 度；
（4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．
已知：如图，AB=AC，BD⊥AC，CE⊥AB，垂足分别为D、E，BD、CE相交于点F，求证：DF=EF．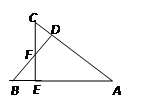
下面是数学课堂的一个学习片断．阅读后，请回答下面的问题：
学习等腰三角形有关内容后，张老师请同学们交流讨论这样一个问题：“已知等腰三角形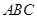
的角
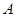等于300，请你求出其余两角”．
同学们经片刻的思考与交流后，李明同学举手讲：“其余两角是300和1200”；
王华同说：“其余两角是750和750”．还有一些同学也提出了不同的看法
．
（1）假如你也在课堂中，你的意见如何？为什么？
（2）通过上面数学问题的讨论，你有什么感受？（用一句话表示）
如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴对称的△A1B1C1，画出△ABC关于x轴对称的△A2B2C2 并写出△A2B2C2的顶点坐标.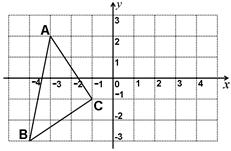
解方程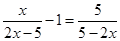
把下列各式因式分解
（1）
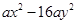（2）