如图，在平面直角坐标系中，直线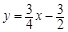
与抛物线
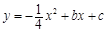交于A、B两点，点A在x轴上，点B的横坐标为－8．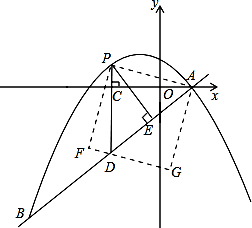
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为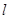
，点P的横坐标为
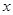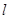，求关于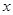的函数关系式，并求出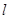的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在
轴上时，求出对应点P的坐标．
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA ，这时sadA=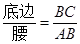
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述关于角的正对定义，解决下列问题：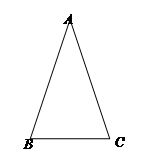
sad
的值为（ ▲）
A． |
B．1 | C． |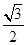
D．2 |
对于
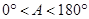，∠A的正对值sadA的取值范围是( ▲ )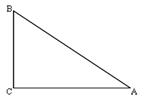
A． |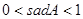
B． |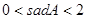
C． |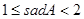
D． |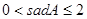
已知，如图，在△ABC中，∠ACB为直角，
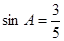，AB=25试求sadA的值
某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：
| A |
B |
|
| 进价（元/件） |
1200 |
1000 |
| 售价（元/件） |
1380 |
1200 |
（注：获利 = 售价 — 进价）该商场购进A、B两种商品各多少件；
商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？
如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．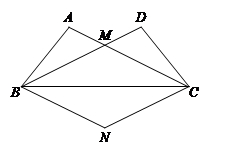
求证：△ABC≌△DCB
过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．
在初三毕业前，团支部进行“送赠言”活动，某班团支部对该班全体团员在一个月内所发赠言条数的情况进行了统计，并制成了如图两幅不完整的统计图：
则该班团员共有▲位，这些团员在这一个月内所发赠言的平均条数是▲，并将该条形统计图补充完整
如果发了3条赠言的同学中有两位男同学，发了4条赠言的同学中有三位女同学．现要从发了3条赠言和4条赠言的同学中分别选出一位参加该校团委组织的“送赠言”活动总结会，请你用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
化简：
，并求a=2时代数式的值．