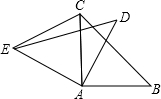
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
(1)求证:PD是⊙O的切线;
(2)若∠CAB=120°,AB=2,求BC的值.
已知:如图,在△ABC中,AB="AC=" 5,BC= 8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
已知关于x的一元二次方程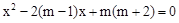 .
.
(1)若此方程有实数根,求m的取值范围;
(2)若x=-1是这个方程的一个根,求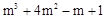 的值.
的值.
已知a,b为实数,且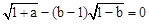 ,求
,求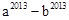 的值.
的值.
如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为160cm2,那么纸板各角应切去边长为多大的正方形?
如图,等腰直角△ABC绕直角顶点A按逆时针方向旋转60°后得到△ADE,且BC=2,求EC的长.