如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．
（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，证明：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．
（3+3＝6分）已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法）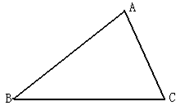
①作∠ABC的平分线BD交AC于点D；
②作线段BD的垂直平分线交AB于点E，交BC于点F。
由（1）、（2）可得：线段EF与线段BD的关系为：.
观察图的点阵图形和与之相对应的等式，探究其中的规律：
（1）请你在④和⑤后面的横线上分别写出相对应的等式；
（2）通过猜想，写出与第n个图形相对应的等式．
某种商品进价m元/件．在销售旺季，该商品售价较进价高30%；销售旺季过后，又以7折（70%）的价格开展促销活动，这时一件商品的售价是多少元？
列代数式：比m的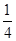
多20%的数．
列代数式：某数x的平方的3倍与y的商；