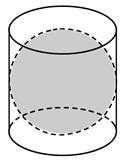
如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )
A.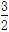 ,1 ,1 |
B.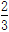 ,1 ,1 |
C.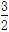 , ,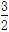 |
D.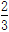 , ,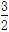 |
离心率为 ,且过点(2,0)的椭圆的标准方程为()
,且过点(2,0)的椭圆的标准方程为()
A. +y2=1或 +y2=1或 + + ="1" ="1" |
B. +y2=1或 +y2=1或 + +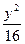 =1 =1 |
C. +y2="1" +y2="1" |
D. + + =1 =1 |
设椭圆的两个焦点分别为F1、F2,过F2作长轴的垂线交椭圆于点P,△PF1F2为等腰直角三角形,则椭圆的离心率为( )
A. |
B. |
C.2- |
D. -1 -1 |
椭圆 =1和
=1和 =k(k>0)具有…( )
=k(k>0)具有…( )
| A.相同的长轴 | B.相同的焦点 |
| C.相同的顶点 | D.相同的离心率 |
已知F1、F2为椭圆 =1(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆离心率e=
=1(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆离心率e= ,则椭圆的方程是( )
,则椭圆的方程是( )
A. ="1" ="1" |
B. =1 =1 |
C. ="1" ="1" |
D. =1 =1 |
椭圆 =1的右焦点为F,设A(-
=1的右焦点为F,设A(- ,3),P是椭圆上一动点,则|AP|+5|PF|取最小值时,P的坐标为( )
,3),P是椭圆上一动点,则|AP|+5|PF|取最小值时,P的坐标为( )
| A.(5,0) | B.(0,2) | C.( ,3) ,3) |
D.(0,-2)或(0,2) |