如图所示,在倾角为37°的固定斜面上静置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8,求:(sin37°=0.6,cos37°=0.8, )
)
(1)物体所受的摩擦力;
(2)若改用沿斜面向上的力拉物体,使之向上匀速运动,则拉力时多少?
如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求: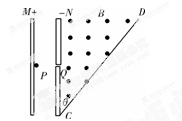
(1)两板间电压的最大值Um;
(2)CD板上可能被粒子打中区域的长度s;
(3)粒子在磁场中运动的最长时间tm.
2014年8月3日我国云南鲁甸发生里氏6.5级地震,为救援灾区人民,要从悬停在空中的直升机上投放救灾物资,每箱救灾物资的质量为20 kg,设箱子承受的地面冲击力大小为1 000 N,箱子与地面的作用时间为0.5 s,已知当地的重力加速度g=10 m/s2,不计空气阻力,试求:
(1)与地面作用时,箱子的加速度是多少?
(2)为保证救灾物资安全落地,飞机投放物资时的高度不应超过多少米?
如图,在大气中有一水平放置的固定圆筒,它由a、b和c三个粗细不同的部分连接而成,各部分的横截面积分别为2S、 S和S。已知大气压强为p0,温度为T0,两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
S和S。已知大气压强为p0,温度为T0,两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
旋转电枢式发电机的转子在正常运转时,产生的电动势瞬时值为e=220 sin314t V.如果由于某种原因,它的转速变慢,用电压表测得此时发电机两端的电压为176 V,若此时发电机正在向一盏标有“220 V、100 W”的灯泡供电,在不计发电机内电阻的情况下,试求:
sin314t V.如果由于某种原因,它的转速变慢,用电压表测得此时发电机两端的电压为176 V,若此时发电机正在向一盏标有“220 V、100 W”的灯泡供电,在不计发电机内电阻的情况下,试求:
(1)该灯泡的实际功率为多大?
(2)这台发电机的转速比原来正常时转速慢了几分之一?
如图,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定量的气体(可视为理想气体),气体温度为T1.开始时,将活塞上方的气体缓慢抽出,当活塞上方的压强达到p0时,活塞下方气体的体积为V1,活塞上方玻璃管的容积为2.6V1。活塞因重力而产生的压强为0.5p0。继续将活塞上方抽成真空并密封.整个抽气过程中管内气体温度始终保持不变.然后将密封的气体缓慢加热.求:活塞刚碰到玻璃管顶部时气体的温度.