下列对牛顿第二定律的表达式F=ma及其变形公式的理解，正确的是（ ）
| A．由F=ma可知，物体所受的合外力与物体的质量成正比，与物体的加速度成反比 |
B．由m= 可知，物体的质量与其所受合外力成正比，与其运动的加速度成反比 |
C．由 可知，物体的加速度与其所受合外力成正比，与其质量成反比 |
| D．由m=可知，物体的质量可以通过测量它的加速度和它所受到的合外力而求得 |
关于运动的合成与分解，下列说法中正确的有：（ ）
| A．两个速度大小不等的匀速直线运动的合运动一定是匀速直线运动 |
| B．两个直线运动的合成一定是直线运动 |
| C．合运动是加速运动时，其分运动中至少有一个是加速运动 |
| D．合运动是匀变速直线运动时其分运动中至少有一个是匀变速直线运动 |
如图所示，从倾角为θ的斜面上的M点水平抛出一个小球，小球的初速度为v0，最后小球落在斜面上的N点，则（ ）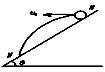
| A．可求M、N之间的距离 |
| B．可求小球落到N点时速度的大小和方向 |
| C．可求小球平抛运动过程动能的变化 |
| D．可以断定，当小球速度方向与斜面平行时，小球与斜面间的距离最大 |
如图7所示，一航天器围绕地球沿椭圆形轨道运动，地球的球心位于该椭圆的一个焦点上，A、B两点分别是航天器运行轨道上的近地点和远地点。若使该航天器由椭圆轨道进入外层的圆轨道（圆轨道与椭圆轨道相切于B点）运行，需要在航天器运行到B位置时再次点火。如果航天器分别在椭圆轨道和圆轨道上正常运行，以下说法正确的是（）
| A．航天器在椭圆轨道上经过B点时的加速度等于它在圆轨道上经过B点时的加速度 |
| B．航天器在椭圆轨道上经过B点时的速度等于它在圆轨道上经过B点时的速度 |
| C．航天器在椭圆轨道上分别经过A、B两点时的速率相等 |
| D．航天器在圆轨道上经过C点时的速率小于它在椭圆轨道上经过A点的速率 |
如图所示，在水平地面上有一倾角为θ的光滑固定斜面体，其上有一小物块A受到一水平向右的推力F的作用。已知物块A沿斜面加速下滑，现保持F的方向不变，使其减小，则物块A的加速度（）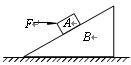
| A．一定变小 | B．一定变大 |
| C．一定不变 | D．可能变小，可能变大，也可能不变 |
如图所示，在水平地面上有一倾角为θ的斜面体B处于静止状态，其斜面上放有与之保持相对静止的物体A。现对斜面体B施加向左的水平推力，使物体A和斜面体B一起向左做加速运动，加速度从零开始逐渐增加，直到A和B开始发生相对运动，关于这个运动过程中A所受斜面的支持力N，以及摩擦力f的大小变化情况，下列说法中正确的是（）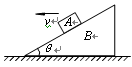
| A．A所受合外力的方向始终是沿水平方向 |
| B．N、f的合力与水平面间的夹角越来越小 |
| C．N、f的合力一定越来越大 |
| D．A对B的作用力越来越小 |