如图（甲），MN、PQ两条平行的光滑金属轨道与水平面成θ = 30°角固定，M、P之间接电阻箱R，电阻箱的阻值范围为0～4Ω，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B = 0.5T。质量为m的金属杆a b水平放置在轨道上，其接入电路的电阻值为r。现从静止释放杆a b，测得最大速度为vm。改变电阻箱的阻值R，得到vm与R的关系如图（乙）所示。已知轨距为L = 2m，重力加速度g=l0m/s2，轨道足够长且电阻不计。
（1）当R = 0时，求杆a b匀速下滑过程中产生感生电动势E的大小及杆中的电流方向；
（2）求金属杆的质量m和阻值r；
（3）求金属杆匀速下滑时电阻箱消耗电功率的最大值Pm。
、一艘宇宙飞船绕一个不知名的、半径为R的行星表面飞行，环绕一周飞行时间为T (万有引力常量为G)，求：该行星的质量M和平均密度ρ
甲、乙两物体在水平面内做匀速圆周运动，半径之比为1：2，相同时间内甲转动20周，乙转动了40周，问甲、乙转动的角速度之比,周期之比,线速度之比为各为多少。
如图所示，质量为M=2kg的平板车静止在光滑水平面上，车的一端静止着质量为MA=1kg的物体A(可视为质点)。一个质量为m=20g的子弹以500m/s的水平速度射穿A后，速度变为200m/s，最后物体A静止在车上。若物体A与小车间的动摩擦因数μ=0.5。
（1）平板车最后的速度是多大？
（2）A在平板车上滑行的距离为多少？
如下图中的实线是一列简谐波在某一时刻的波形曲线, 经0.5 s以后，其波形如图中的虚线所示，在该0.5 s内，图中质点运动的路程小于6 cm。
⑴如果波向右传播，那么波速是多大？周期是多大？
⑵如果波向左传播，那么波速可能是多大？周期可能是多大？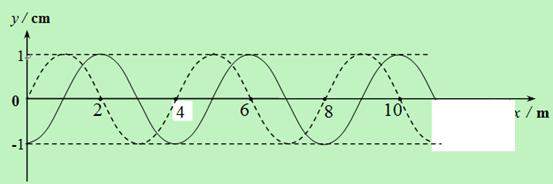
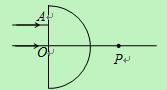
两束平行的细激光束，垂直于半圆柱玻璃的平面射到半圆柱玻璃上，如图所示。已知其中一条光线沿直线穿过玻璃，它的入射点是O；另一条光线的入射点为A，穿过玻璃后两条光线交于P点。已知玻璃截面的圆半径为R，OA=
，OP=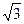
R，求玻璃材料的折射率。