阅读一段文字，再回答下列问题：已知在平面内两点的坐标为P1（x1，y1），P2（x2，y2），则该两点间距离公式为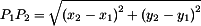
．同时，当两点在同一坐标轴上或所在直线平行于x轴、垂直于x轴时，两点间的距离公式可化简成|x2－x1|或|y2－y1|．
（1）若已知两点A（3，3），B（－2，－1），试求A，B两点间的距离；
（2）已知点M，N在平行于y轴的直线上，点M的纵坐标为7，点N的纵坐标为－2，试求M，N两点间的距离；
（3）已知一个三角形各顶点的坐标为A（0，5），B（－3，2），C（3，2），你能判定此三角形的形状吗？试说明理由．
列方程解应用题
福州市某楼盘准备以每平方米10000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米8100元的均价开盘销售．
（1）求平均每次下调的百分率；
（2）某人准备以开盘均价购买一套100平方米的房子．开发商还给予以下两种优惠方案以供选择：①打9.9折销售；②不打折，送两年物业管理费．物业管理费是每平方米每月1元．请问哪种方案更优惠？
在直径为100cm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=80cm，求油的最大深度。
如图，在网格中有一个四边形的图案。．
（1）请你画出此图案绕点O顺时针方向旋转90°，180°，270°的图案，你会得到一个美丽的图案，千万不要将阴影位置涂错；
（2）若网格中每个小正方形的边长为1，旋转后点
的对应点依次为
，
，
，求四边形
的面积；
（3）这个美丽图案能够证明一个我们学过的著名定理，请直接写出这个定理名称，不要求证明。
已知
，
，试求
的值。
按要求解方程：（每小题5分，共20分）
（1）
(2)
(3)
(公式法) (4)
（配方法）