某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2．5倍，再作3次降价处理；第一次降价30％，标出“亏本价”；第二次降价30％，标出“破产价”；第三次降价30%，标出“跳楼价”．3次降价处理销售结果如下表：
| 降价次数 |
一 |
二 |
三 |
| 销售件数 |
10 |
40 |
一抢而光 |
（1）跳楼价占原价的百分比是多少?
（2）该商品按新销售方案销售，相比原价全部售完，哪种方案更盈利?
解方程
（1）4x-1．5x=-0．5x-9；
（2）1-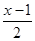
=2-
．
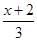计算题：
（1）（-2）4÷（-2
）+5
×（-
）-0．25；
（2）（2a2-5a）-2（-3a+5+a2）．
小明同学做一道题“已知两个多项式A、B，计算
”，小黄误将看作
，求得结果是C．若
，
，请你帮助小明求出的正确答案．
有理数a、b、c在数轴上的对应点如图，化简代数式：
=_________．
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元。厂方在开展促销活动期间，向客户提供两种优惠方案：①西装和领带都按定价的90％付款；②买一套西装送一条领带．现某客户要到该服装厂购买x套西装（x≥1），领带条数是西装套数的4倍多5．
（1）若该客户按方案①购买，需付款________________元；（用含x的代数式表示）
若该客户按方案②购买，需付款______________元。（用含x的代数式表示）
（2）若x=10，通过计算说明此时按哪种方案购买较为合算?