已知函数 对任意实数
对任意实数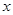 ,
, 恒有
恒有 ,且当
,且当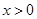 时,
时,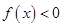 ,又
,又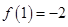 .
.
(1)判断 的奇偶性;
的奇偶性;
(2)求证: 是
是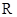 上的减函数;
上的减函数;
(3)求 在区间
在区间 上的值域;
上的值域;
(4)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知 数列
数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线 上
上 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前n项和为且
的前n项和为且 满足
满足 ,试确定
,试确定 的值,使得数列
的值,使得数列 是等差数列;
是等差数列;
(3)求证: .
.
设 表示的区域为A,
表示的区域为A,
(1)在区域A中任取一点(x,y),求 的取值范围;
的取值范围;
(2)平面上有一定点O(3,3),若一动点M满足 ,求点M落入区域A内的概率。
,求点M落入区域A内的概率。
本地一公司计划2011年在省、市两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,省、市电视台的广告收费标准分别为 元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
某校高二文科分为四个班,期中测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人,抽取出来的所有学生的测试成绩统计结果的频率分布的条形图如图所示,其中120-130(包括120分但不包括130分的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少?
(2)在抽取的所有学生中,任取一名,求分数不少于90分的概率.
已知向量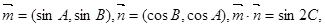 且A、B、C分别为△ABC的三边a、b、c所对的角.
且A、B、C分别为△ABC的三边a、b、c所对的角.
(1)求角C的大小;
(2)若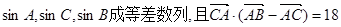 ,求c边的长.
,求c边的长.