(本小题满分10分)已知数列 的前
的前 项和为
项和为 ,
, ,
,
(I)求数列 的通项公式;
的通项公式;
(II)设 ,求
,求 的值.
的值.
(本小题满分10分)一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成 夹角的方向继续飞行
夹角的方向继续飞行 直到终点.这样飞机的飞行路程比原来路程700km远了多少?(
直到终点.这样飞机的飞行路程比原来路程700km远了多少?( )
)
|

(本小题满分12分)已知关于的一元二次函数 ,(1)设集合
,(1)设集合 ,分别从集合
,分别从集合 和
和 中随机取一个数为
中随机取一个数为 和
和 ,求函数
,求函数 在区间
在区间 上是增函数的概率;(2)设点
上是增函数的概率;(2)设点 是区域
是区域
 内的随机点,
内的随机点,
求函数 在区间
在区间 上是增函数的概率
上是增函数的概率
选修4-5:不等式选讲
已知函数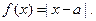 不等式
不等式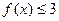 的解集为
的解集为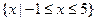
(1)求实数a的值;
(2)若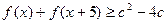 对一切实数x恒成立,求实数c的取值范围。
对一切实数x恒成立,求实数c的取值范围。
选修4-1:几何证明选讲
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交于⊙O于点E,D,连接EC,CD。
(1)试判断直线AB与⊙O的位置关系,并加以证明;
(2)若 ,⊙O的半径为3,求OA的长。
,⊙O的半径为3,求OA的长。