下图是2006年某省各类学校在校生数情况制作的扇形统计图和不完整的条形统计图.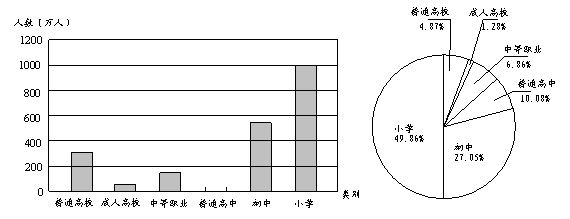
已知2006年该省普通高校在校生为97.41万人,请根据统计图中提供的信息解答下列问题:
(1)2006年该省各类学校在校生总人数约多少万人?(精确到1万)
(2)补全条形统计图;
(3)请你写出一条合理化建议.
如图,点E、F、G分别 是□ABCD的边AB、BC、CD、DA的中点.求证:ΔBEF≌ΔDGH.
如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与 轴相交于点A,与
轴相交于点A,与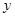 轴相交于点B。
轴相交于点B。
(1)点P在运动时,线段AB的长度页在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q、O、A、P为顶点的四边形时平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由。
在平面直角坐标系中,已知二次函数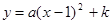 的图像与
的图像与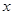 轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准: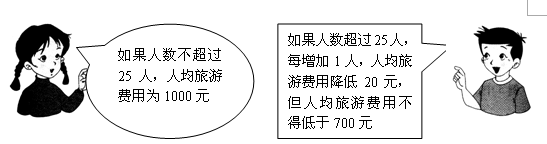 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?