如图所示电路,电灯R1=24Ω,电动机绕组的电阻R0=1Ω,当电键S1、S2闭合时,测得电阻R1的电功率是P=96W,理想电流表的读数为I=5A,求此时:
(1)电源的输出功率;
(2)电动机的输出功率.
如图所示,某种自动洗衣机进水时,洗衣机缸内水位升高,与洗衣缸相连的细管中会封闭一定质量的空气(可视为理想气体),通过压力传感器可感知管中的空气压力,从而控制进水量.若进水前细管内空气的体积为 ,压强为
,压强为 ,当洗衣缸内水位缓慢升高(假设细管内空气温度不变),被封闭空气的压强变为
,当洗衣缸内水位缓慢升高(假设细管内空气温度不变),被封闭空气的压强变为 时(
时( >1).求:细管内进水的体积.
>1).求:细管内进水的体积.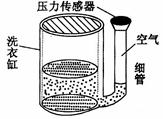
如图所示,BCDG是光滑绝缘的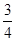 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为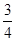 mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.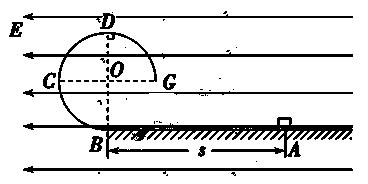
(1)若滑块从水平轨道上距离B点s=3R的A点由静止释放,滑块到达与圆心O等高的C点时速度为多大?
(2)在(1)的情况下,求滑块到达C点时受到轨道的作用力大小;
(3)改变s的大小,使滑块恰好始终沿轨道滑行,且从G点飞出轨道,求滑块在圆轨道上滑行过程中的最小速度大小.
如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知AB间距离s1=0.4 m,g=10 m/s2.求: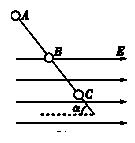
(1)小球在B点的速度vB .
(2)小球进入电场后滑行的最大距离s2 .
(3)小球从A点滑至C点的时间是多少?
如图所示,一根长为 的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求: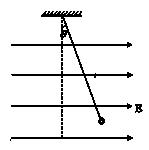
(1)小球带何种电荷,带电量为多少;
(2)如果将细线剪断,小球经时间t发生的位移大小;
(3) 若将小球拉至最低点无初速释放,当小球运动到图示位置时受到线的拉力的大小。
如图所示,一根柔软的弹性绳子右端固定在竖直墙壁上,现在绳上每隔0.20m标记一个点,分别记为A、B、C、D、E…,拉着绳子的左端点A使其上下做简谐运动时,绳上便形成一列向右传播的简谐横波.若A点从平衡位置开始起振,且经0.2s第一次达到最大位移处,此时C点恰好开始振动.求:简谐振动周期和波的传播速度.