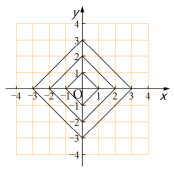
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的数.
(1)画出由里向外的第 个正方形,求在第四个正方形边上有多少个整点?
(2)请你猜测由里向外第 个正方形(实线)四条边上的整点共有多少个;
(3)探究点 在由里向外的第几个正方形的边上,点 在由里向外的第几个正方形的边上.
如图,将长方形 放置在平面直角坐标系中, 轴,且 ,且 .
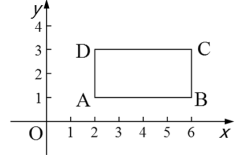
(1)求 的坐标,并说明将长方形 进行怎样的平移使 点移到 点处;
(2) 轴上是否存在点 ,使 的面积等于长方形 面积的 ,若存在,求出 点坐标;若不存在,说明理由.
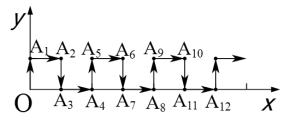
在平面直角坐标系中,一蚂蚁从原点 出发,按向上、向右、向下、向右方向依次不断移动,每次移动 个单位,其行走路线如图所示.
(1)填写下列各点的坐标:
( ), ( ), ( )
(2)写出点 的坐标( 是正整数);
(3)指出蚂蚁从点 到点 的移动方向.
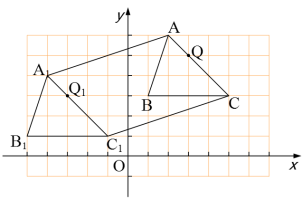
如图所示, 是由 平移后得到的,已知 中任意一点 经平移后对应点为 .
(1)已知 ,请写出 的坐标
(2)试说明 是如何由 得到的?
(3)连接 ,求出五边形 的面积.
已知 是整数,求所有满足条件的正整数 的和.