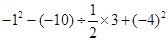下表给出了某班6名同学身高情况（单位：cm）
（1）完成表中空的部分；
（2）他们6人中最高身高比最矮身高高多少？
（3）如果身高达到或超过平均身高时叫达标身高，那么这6个同学身高的达标率是多少？（精确到小数点后两位）
如图，已知∠1+∠D=90°，BE∥FC，且DF⊥BE与点G，并分别于AB、CD交于点F、D，求证：AB∥CD．
已知
、
互为相反数且
，
、
互为倒数，
的绝对值是最小的正整数，
求
的值． （注：
=
）
解：∵、互为相反数且，∴
__________，
__________；
又∵、互为倒数，∴
__________；
又∵的绝对值是最小的正整数， ∴
__________，∴
__________；
∴原式
__________．
某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有n张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？
解方程
（1）
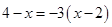
（2）
计算：
（1）
（2）
（3）
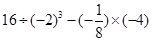
（4）