下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,...,按此规律排列,则第⑦个图形中小圆圈的个数为()
| A.21 | B.24 | C.27 | D.30 |
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是()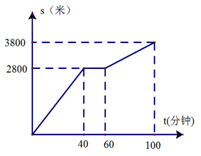
| A.小明中途休息用了20分钟 |
| B.小明休息前爬山的平均速度为每分钟70米 |
| C.小明在上述过程中所走的路程为6600米 |
| D.小明休息前爬山的平均速度大于休息后爬山的平均速度 |
如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若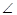 AOC=80°,则
AOC=80°,则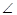 ADB的度数为()
ADB的度数为()
A.40° B.50° C.60° D.20°
一元二次方程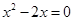 的根是()
的根是()
A. |
B.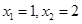 |
C. |
D.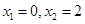 |
在某校九年级二班组织的跳绳比赛中,第一小组五位同学跳绳的个数分别为198,230,220,216,209,则这五个数据的中位数为()
| A.220 | B.218 | C.216 | D.209 |