如图，一个点从数轴上的原点开始，先向左移动
到达
点，再向左移动
到达
点，然后向右移动
到达
点．
（1）用1个单位长度表示
，请你在数轴上表示出、、三点的位置；
（2）把点到点的距离记为
，则= 
．
（3）阅读理解：观察式子：
因此可以得到：括号前面是“－”号，把括号和它前面的“－”号去掉，括号里各项都改变正负号．
问题解决
若点以每秒的速度向左移动，同时、点分别以每秒、
的速度向右移动．设移动时间为
秒,试探索：
的值是否会随着的变化而改变？请说明理由．
如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD，连结BD、CE，相交于O.（1）试写出图中和BD相等的一条线段并说明你的理由；（2）求出BD和CE的夹角大小，若改变△ABC的形状，这个夹角的度数会发生变化吗？请说明理由.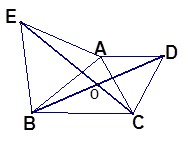
已知：如图，∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于D，AD=2.5cm，DE=1.7cm，求BE的长。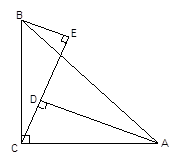
如图，△ABC中，∠A＝30°，
＝90°，BE平分∠ABC，AC＝9cm，求CE的长。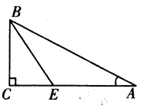
如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF.求证：AD平分∠BAC．
如图，点B，D，C，F在一条直线上，且BC＝FD，AB＝EF．
（1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是；
（2）添加了条件后，证明△ABC≌△EFD。