如图所示,为一轻质弹簧的长度和弹力大小的关系.根据图象判断,正确的结论是( )
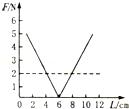
| A.弹簧的劲度系数为1 N/m |
| B.弹簧的劲度系数为100 N/m |
| C.弹簧的原长为6 cm |
| D.弹簧伸长0.2 m时,弹力的大小为4 N |
在国际单位制中,长度、质量和时间三个基本物理量的基本单位是()
| A.米、千克和秒 | B.米、克和秒 |
| C.千米、克和小时 | D.千米、千克和小时 |
如图所示,某“闯关游戏”的笔直通道上每隔8m设有一个关卡,各关卡同步放行和关闭,放行和关闭的时间分别为5s和2s.关卡刚放行时,一同学立即在关卡1处以加速度2 m/s2由静止加速到2 m/s,然后匀速向前,则最先挡住他前进的关卡是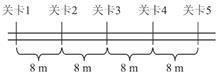
| A.关卡5 | B.关卡4 | C.关卡3 | D.关卡2 |
如图所示,质量为m的滑块静止置于倾角为30°的粗糙斜面上,一根轻弹簧一端固定在竖直墙上的P点,另一端系在滑块上,弹簧与竖直方向的夹角为30°,则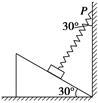
| A.弹簧一定处于压缩状态 |
| B.斜面对滑块的支持力大小可能为零 |
| C.滑块可能受到三个力作用 |
D.斜面对滑块的摩擦力大小一定等于 mg mg |
如图所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中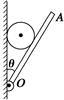
| A.小球对墙的压力减小 |
| B.小球对薄板的压力增大 |
| C.小球对墙的压力先减小后增大 |
| D.小球对薄板的压力不可能小于球的重力 |
一辆公共汽车进站后开始刹车,做匀减速直线运动.开始刹车后的第1 s内和第2 s内位移大小依次为9 m和7 m.则刹车后6 s内的位移是
| A.20 m | B.24 m | C.25 m | D.75 m |