(本小题满分16分)
经市场调查,某超市的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间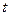 (天)的函数,且日销售量近似满足
(天)的函数,且日销售量近似满足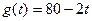 (件),价格近似满足
(件),价格近似满足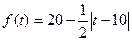 (元).
(元).
(Ⅰ)试写出该种商品的日销售额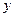 与时间
与时间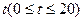 的函数表达式;
的函数表达式;
(Ⅱ)求该种商品的日销售额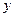 的最大值与最小值.
的最大值与最小值.
(本小题满分14分)
设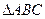 的三个内角
的三个内角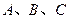 所对的边分别为
所对的边分别为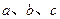 ,且满足
,且满足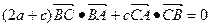 .
.
(Ⅰ)求角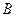 的大小;
的大小;
(Ⅱ)若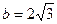 ,试求
,试求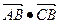 的最小值.
的最小值.
(本小题满分14分)
设不等式组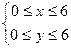 表示的区域为A,不等式组
表示的区域为A,不等式组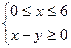 表示的区域为B,在区域A中任意取一点
表示的区域为B,在区域A中任意取一点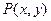 .
.
(Ⅰ)求点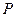 落在区域
落在区域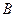 中概率;
中概率;
(Ⅱ)若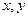 分别表示甲、乙两人各掷一次正方体骰子向上的面所得的点数,求点
分别表示甲、乙两人各掷一次正方体骰子向上的面所得的点数,求点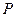 落在区域
落在区域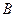 中的概率.
中的概率.
(本小题满分14分)
已知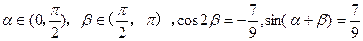 .
.
(Ⅰ)求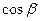 的值;
的值;
(Ⅱ)求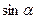 的值.
的值.
(本小题满分14分)已知:对于数列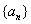 ,定义
,定义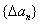 为数列
为数列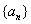 的一阶差分数列,其中
的一阶差分数列,其中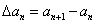 , (1)若数列
, (1)若数列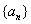 的通项公式
的通项公式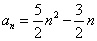 (
(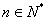 ),求:数列
),求:数列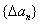 的通项公式; (2)若数列
的通项公式; (2)若数列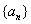 的首项是1,且满足
的首项是1,且满足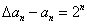 ,
,
①设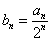 ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
②求:数列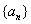 的通项公式及前
的通项公式及前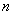 项和
项和