某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图.

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?

(注: ,n=a+b+c+d)
,n=a+b+c+d)
| |
生产能手 |
非生产能手 |
合计 |
| 25周岁以上组 |
|
|
|
| 25周岁以下组 |
|
|
|
| 合计 |
|
|
|
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
(Ⅰ)若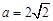 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(Ⅱ)求实数a的值,使得二面角A-EC-D的大小为60°.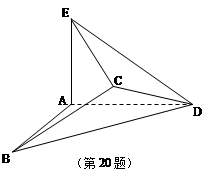
设数列 {an} 中,a1=a,an+1+2an=2n+1(n∈N*).
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列 {an} 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由.
已知函数 f (x)=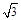 sinωx+
sinωx+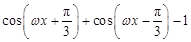 (ω>0,x∈R),且函数 f (x) 的最小正周期为π.
(ω>0,x∈R),且函数 f (x) 的最小正周期为π.
(Ⅰ)求函数 f (x) 的解析式;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c.若f (B)=1, ,
,
且a+c=4,试求b2的值.
在平面直角坐标系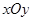 中,椭圆
中,椭圆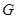 的中心为坐标原点,左焦点为
的中心为坐标原点,左焦点为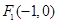 ,
,  为椭圆
为椭圆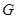 的上顶点,且
的上顶点,且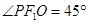 .
.
(Ⅰ)求椭圆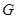 的标准方程;
的标准方程;
(Ⅱ)已知直线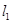 :
: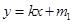 与椭圆
与椭圆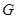 交于
交于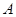 ,
, 两点,直线
两点,直线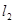 :
: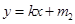 (
(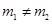 )与椭圆
)与椭圆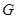 交于
交于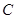 ,
,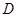 两点,且
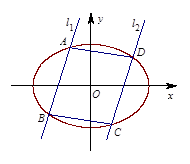
两点,且 ,如图所示.
,如图所示.
(ⅰ)证明: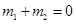 ;
;
(ⅱ)求四边形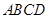 的面积
的面积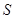 的最大值.
的最大值.
已知函数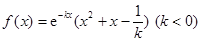 .
.
(Ⅰ)求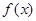 的单调区间;
的单调区间;
(Ⅱ)是否存在实数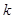 ,使得函数
,使得函数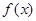 的极大值等于
的极大值等于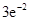 ?若存在,求出
?若存在,求出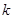 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.