设函数 ,其中
,其中 ,曲线
,曲线 恒与
恒与 轴相切于坐标原点.
轴相切于坐标原点.
(1)求常数 的值;
的值;
(2)当 时,关于
时,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证: .
.
(本小题满分10分)
已知函数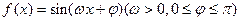 为偶函数,其图象上相邻的两个最高点之间的距离为
为偶函数,其图象上相邻的两个最高点之间的距离为
(1)求 的解析式;
的解析式;
(2)若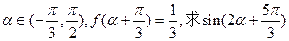 的值。
的值。
(本小题满分16分)
已知数列 满足,
满足,
(1)若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)当 时,求数列
时,求数列 的前n项和
的前n项和 ;
;
(3)若对任意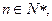 都有
都有 成立,求
成立,求 的取值范围.
的取值范围.
(本小题满分16分)
已知圆M的圆心M在y轴上,半径为1.直线 被圆M所截得的弦长为
被圆M所截得的弦长为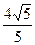 ,且圆心M在直线
,且圆心M在直线 的下方.
的下方.
(1)求圆M的方程;
(2)设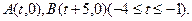 若AC,BC是圆M的切线,求
若AC,BC是圆M的切线,求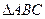 面积的最小值.
面积的最小值.
(本小题满分16分)
已知函数 且
且 ,其中
,其中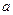 、
、
(1)求m的值;
(2)求函数 的单调增区间.
的单调增区间.
(本小题满分14分)
某专卖店经市场调查得知,一种商品的月销售量Q(单位:吨)与销售价格 (单位:万元/吨)的关系可用下图的一条折线表示.
(单位:万元/吨)的关系可用下图的一条折线表示.
(1)写出月销售量Q关于销售价格 的函数关系;
的函数关系;
(2)如果该商品的进价为5万元/吨 ,除
,除 去进货成本外,专卖店销售该商品每月的固定成本为10万元,问该商品每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
去进货成本外,专卖店销售该商品每月的固定成本为10万元,问该商品每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.