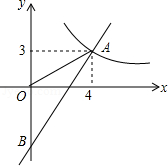
如图,一次函数的图象分别与反比例函数的图象在第一象限交于点,与轴的负半轴交于点,且.
(1)求函数和的表达式;
(2)已知点,试在该一次函数图象上确定一点,使得,求此时点的坐标.
先阅读,再解答:
我们在判断点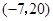 是否在直线
是否在直线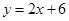 上时,常用的方法:把
上时,常用的方法:把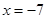 代入
代入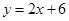 中,由
中,由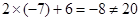 ,判断出点
,判断出点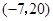 不在直线
不在直线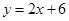 上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由
上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由
为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.求每年市政府投资的增长率;
若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,求m的值.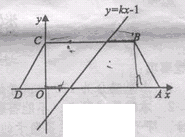
用两个全等的正方形 和
和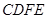 拼成一个矩形
拼成一个矩形 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边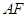 的中点
的中点 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点 按逆时针方向旋转
按逆时针方向旋转
当直角三角尺的两直角边分别与矩形
 的两边
的两边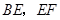 相交于点
相交于点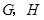 时,如图甲,通过观察或测量
时,如图甲,通过观察或测量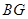 与
与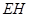 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.当直角三角尺的两直角边分别与
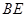 的延长线,
的延长线,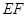 的延长线相交于点
的延长线相交于点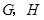 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
、(12分)正式足球比赛对所用足球的质量有严格规定,标准质量为400克,下面是5个足球的质量检测结果(用正数记超过规定质量的克数,用负数记不足规定质量的克数):
①、―25②+10③-20④+30⑤+15
(1)写出每个足球的质量
(2)请指出哪个足球(指出序号)的质量好一些,请用绝对值的知识说明。