图1,图2都是的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点
(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);
(2)图1中所画的平行四边形的面积为 .

已知:如图,在等腰梯形ABCD中,AD∥BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.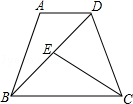
证明:△ADB≌△EBC
某班观看电影《和雷锋在一起的日子》,有甲、乙两种电影票,甲种票每张24元,乙种票每张18元.如果全班35名同学购票用去750元,那么甲、乙两种电影票各多少张?
某中学在近日组织师生共900人举行以“感受春天,亲近自然,收获快乐”为主题的春游活动,为此学校决定到野生动物园游览.为确保师生活动安全(如校车等安全),学校、旅行社和相关部分充分协商决定,本次春游费用为:教师每位120元,学生每位100元.该学校共花费91200元,请问在这次春游活动中,教师和学生各有多少人?
某人家的电话号码是八位数,将前四位数组成的数与后四位数组成的数相加得14405,将前三位数组成的数与后五位数组成的数相加得16970,求此人家的电话号码.
观察下图,回答下列问题:
(1)在图①中有几个角?
(2)在图②中有几个角?
(3)在图③中有几个角?
(4)以此类推,如图④所示,若一个角内有n条射线,此时共有多少个角?