如图①,在中,,,,点从点出发,沿折线向终点运动,在上以每秒5个单位长度的速度运动,在上以每秒3个单位长度的速度运动,点从点出发,沿方向以每秒个单位长度的速度运动,,两点同时出发,当点停止时,点也随之停止.设点运动的时间为秒.
(1)求线段的长;(用含的代数式表示)
(2)连结,当与的一边平行时,求的值;
(3)如图②,过点作于点,以,为邻边作矩形,点为的中点,连结.设矩形与重叠部分图形的面积为.①当点在线段上运动时,求与之间的函数关系式;②直接写出将矩形分成两部分的面积比为时的值.
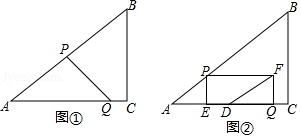
(1)阅读下列解答过程,
求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,
所以y2+4y+8的最小值是4.
(2)仿(1)求①、m2+m+4的最小值②、4-x2+2x的最大值.
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:
(1)从点A出发在图中画一条线段AB,使得AB= ;
;
(2)画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.
某户住房的结构如图所示,该户主人打算把卧室以外的部分都铺上某种地砖,至少需要多少平方米的地砖?如果这种地砖的价格是a元/m2,那么购买所需的地砖至少需要多少元?
已知x、y满足 +|x-2y+2|=0,求x-
+|x-2y+2|=0,求x- y的平方根.
y的平方根.
先化简,再求值:[(2xy-3)(2xy+3)+(xy+3)2]÷xy,
其中x=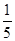 ,y=-2.
,y=-2.