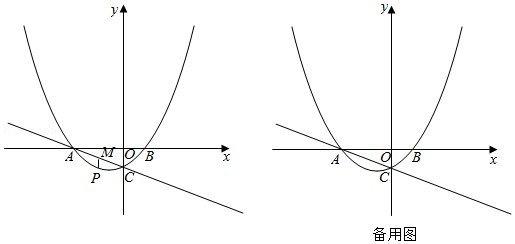
如图,抛物线交轴于,两点,交轴于点.直线经过点,.
(1)求抛物线的解析式;
(2)点是抛物线上一动点,过点作轴的垂线,交直线于点,设点的横坐标为.
①当是直角三角形时,求点的坐标;
②作点关于点的对称点,则平面内存在直线,使点,,到该直线的距离都相等.当点在轴右侧的抛物线上,且与点不重合时,请直接写出直线的解析式.,可用含的式子表示)
如图,在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,BE=6,CD= ,求∠DCB的度数.
,求∠DCB的度数. 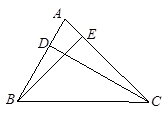
已知:函数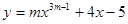 是二次函数.
是二次函数.(1)求m的值;
(2)写出这个二次函数图象的对称轴:,顶点坐标:;
(3)求图象与
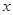 轴的交点坐标.
轴的交点坐标.
(本小题9分)如图,在直角坐标系xoy中,点A(2,0),点B在第一象限且△OAB为等边三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D
(1)判断点C是否为弧OB的中点?并说明理由;
(2)求B、C两点的坐标;
(3)求直线CD的函数解析式;
(4)点P在线段OB上,且满足四边形OPCD是等腰梯形,求点P坐标.
(本小题10分)如图,抛物线 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程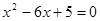 的两个实数根.
的两个实数根.
(1)求A、B两点的坐标;
(2) 求出此抛物线的的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
(本小题8分)如图,AB为⊙O的直径,割线PCD交⊙O于C、D,  .
.
(1)求证:PA是⊙O的切线;
(2)若PA=6,CD=3PC,求PD的长.