如图,已知⊙O中,半径OA⊥OB,则圆周角∠ACB是()
| A.45º | B.90º | C.60º | D.30º |
将函数y=2x2的图象向左平移1个单位,再向上平移3个单位,可得到的抛物线是()
| A.y=2(x-1)2-3 | B.y=2(x-1)2+3 |
| C.y=2(x+1)2-3 | D.y=2(x+1)2+3 |
“a 是实数, ≥0”,这一事件是()
≥0”,这一事件是()
| A.必然事件 | B.不确定事件 | C.不可能事件 | D.随机事件 |
如图,在△ABC中,AB=AC=a,BC=b(a>b)。在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE,则EF等于()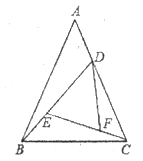
A.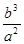 |
B.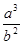 |
C.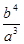 |
D.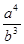 |
如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处。若AB=3,AD=4,则ED的长为()
A.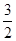 |
B.3 | C.1 | D.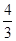 |