我省某苹果基地销售优质苹果,该基地对需要送货且购买量在 (含 和 的客户有两种销售方案(客户只能选择其中一种方案)
方案 :每千克5.8元,由基地免费送货.
方案 :每千克5元,客户需支付运费2000元.
(1)请分别写出按方案 ,方案 购买这种苹果的应付款 (元 与购买量 之间的函数表达式;
(2)求购买量 在什么范围时,选用方案 比方案 付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

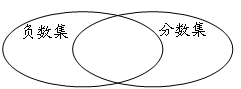
(1)如图,两个圈分别表示负数集和分数集,请将﹣50%,2012,0.618,﹣3, ,0,5.9,﹣3.14,﹣92中,符合要求的数填入相应的圈中;
,0,5.9,﹣3.14,﹣92中,符合要求的数填入相应的圈中;
(2)在数轴上表示下列四个数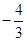 ,
,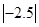 ,0,
,0,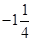 ,并把它们用“<”号连接起来.
,并把它们用“<”号连接起来.
(1) (2)
(2)
某织布厂有工人200名,为改善经营,增设制衣项目,已知每人每天能织布30米,或利用所织布制衣4件,制衣一件用布1.5米,将布直接出售,每米布可获利2元;将布制成衣后出售,每件可获利25元,若每名工人一天只能做一项工作,且不计其他因素,设安排x名工人制衣,那么:
(1)一天中制衣所获得的利润为P=___________________(试用含x的代数式表示并化简);
(2)一天中剩余布出售所获利润为Q=________________(试用含x的代数式表示并化简);
(3)当安排166名工人制衣时,所获总利润是多少元?能否安排167名工人制衣以提高利润? 试说明理由.(本题6分)
有理数a、b、c在数轴上的对应点如图所示:
化简代数式: .
.
先化简,再求值:
(1) ,其中:
,其中: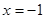 ,
, 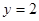 .
.
(2)已知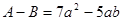 ,且
,且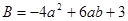 .
.
①求A等于多少;②若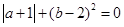 ,求A的值.
,求A的值.
(3)已知多项式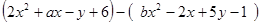 .
.
①若多项式的值与字母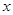 的取值无关,求
的取值无关,求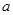 、
、 的值;
的值;
②在①的条件下,先化简多项式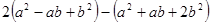 ,再求它的值.
,再求它的值.
化简:(1)
(2)