公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ,导致了第一次数学危机, 是无理数的证明如下:
假设 是有理数,那么它可以表示成 与 是互质的两个正整数).于是 ,所以, .于是 是偶数,进而 是偶数,从而可设 ,所以 , ,于是可得 也是偶数.这与" 与 是互质的两个正整数"矛盾.从而可知" 是有理数"的假设不成立,所以, 是无理数.
这种证明" 是无理数"的方法是
| A. |
综合法 |
B. |
反证法 |
C. |
举反例法 |
D. |
数学归纳法 |
三个数: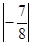 、+
、+ 、
、 的大小关系是()
的大小关系是()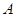 .
. 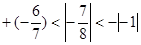
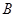 .
. 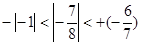
 .
.
 .
.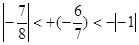
如果某商场盈利5万记作+5万元,那么亏损2万元,应记作() . -2万元
. -2万元 .-2
.-2 .+2万元
.+2万元
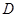 .以上都不对
.以上都不对
有理数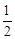 的相反数是 ( )
的相反数是 ( )
| A.2 | B.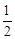 |
C.-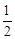 |
D.-2 |
将长方形纸片ABCD(如图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AFE的度数为 ( ) 
若等腰三角形中相等的两边长为10 cm,第三边长为16 cm,那么第三边上的高为 ( )
| A.12 cm | B.10 cm | C.8 cm | D.6 cm |