某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整).
课题 |
测量旗杆的高度 |
|||
成员 |
组长: 组员:,, |
|||
测量工具 |
测量角度的仪器,皮尺等 |
|||
测量示意图 |
|
说明:线段表示学校旗杆,测量角度的仪器的高度,测点,与在同一条水平直线上,,之间的距离可以直接测得,且点,,,,,都在同一竖直平面内,点,,在同一条直线上,点在 上. |
||
测量数据 |
测量项目 |
第一次 |
第二次 |
平均值 |
的度数 |
||||
的度数 |
||||
,之间的距离 |
||||
任务一:两次测量,之间的距离的平均值是 .
任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度.
(参考数据:,,,,,
任务三:该“综合与实践”小组在制定方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)

如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE= CD,求证:DB=DE
CD,求证:DB=DE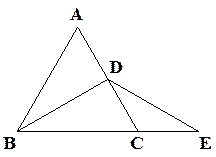
如果,AC⊥BC,BD⊥AD,AC=BD,求证BC=AD。
已知一次函数的图像经过点(-2,5),并且与直线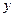 =3
=3 -4相交于
-4相交于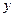
 轴上,求此函数的解析式
轴上,求此函数的解析式
如图,A、B是两个蓄水池,都在河边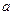 的同侧,为了方便灌溉农作物,要在河边建一个抽水站,将河水送到A、B两地。问该站建在河边什么地方,可使所修
的同侧,为了方便灌溉农作物,要在河边建一个抽水站,将河水送到A、B两地。问该站建在河边什么地方,可使所修 的渠道最短?试
的渠道最短?试 在图中确定该点。(保留作图痕迹)
在图中确定该点。(保留作图痕迹)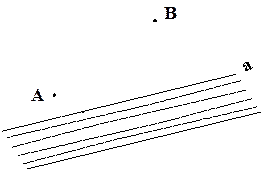
如图,直线y = kx+6与x轴y轴分别相交于点E、F. 点E的坐标为(- 8, 0), 点A的坐标为(- 6,0). 点P(x,y)是第二象限内的直线上的一个动点。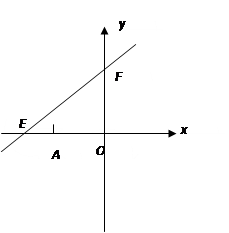
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置(求P的坐标)时,△OPA的面积为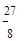 ,并说明理由
,并说明理由