公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元
（Ⅰ）设租用甲种货车 辆 为非负整数），试填写表格．
表一：
租用甲种货车的数量 辆 |
3 |
7 |
|
租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二：
租用甲种货车的数量 辆 |
3 |
7 |
|
租用甲种货车的费用 元 |
|
2800 |
|
租用乙种货车的费用 元 |
|
280 |
|
（Ⅱ）给出能完成此项运送任务的最节省费用的租车方案，并说明理由．
某长甲车间人数比乙车间人数的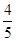
还少30人，如果从乙车间调10人到甲车间，那么甲车间的人数是乙车间的
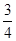，求两个车间原来各有多少人？
政府根据社会需要，对自来水价格举行了听证会，决定从今年4月份起对自来水价格进行调整，调整后生活用水价格的部分信息如下表：
| 用水量（m3） |
单价（元∕m3） |
| 5m3以内（包括5m3）的部分 |
2 |
| 5m3以上的部分 |
 |
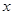已知5月份小晶家和小磊家分别交水费19元、31元，且小磊家的用水量是小晶家的用水量的1.5倍，请你通过上述信息，求出表中的。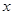
“种粮补贴”惠农政策的出台，大大激发了农民的种粮积极性，某粮食生产专业户去年计划生产小麦和玉米共18t，实际生产了20t，其中小麦超产12%，玉米超产10%，则该专业户去年实际生产小麦、玉米各多少吨？
某商场正在热销2008年奥运会吉祥物“福娃”玩具和徽章两种奥运商品，根据下图提供的信息，求一盒“福娃”玩具和一枚徽章的价格各是多少元？
如图，某铁路MN和公路PQ相交于点O，且交角为90°,某仓库G在A区，到公路、铁路距离相等(即G在∠NOQ的平分线上)，且到公路与铁路的相交点O的距离为200m.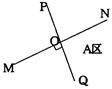
(1)在图上标出仓库G的位置(比例尺1∶10000,用圆规作图，保留作图痕迹，不写作法)：
(2)求出仓库G到铁路的实际距离.