如图,甲、乙两座建筑物的水平距离为,从甲的顶部处测得乙的顶部处的俯角为,测得底部处的俯角为,求甲、乙建筑物的高度和(结果取整数).参考数据:,.

(本小题共4分)小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
(3)从中取出2张卡片,使这2张卡片上数字组成一个最大的数,如何抽取?最大的数是多少?(4)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子.(写出一种即可).
按下面方法折线,然后回答问题: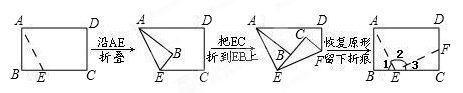
(1)∠2是多少度的角,为什么?
(2)∠1与∠3有何关系,为什么?
(本小题共6分)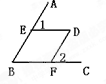
如图, 已知ED∥CB,FD//BE,∠1=500 求∠2的度数?
如图,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,求∠BOD的度数。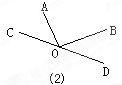
(本小题共6分)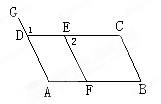
如图,点E在CD上,点F在BA上,G是AD延长线上一点.  (1)若∠A
(1)若∠A =∠1,则可判断_______∥_______,因为________.
=∠1,则可判断_______∥_______,因为________.
(2)若∠1=∠_______,则可判断AG∥BC,因为_________.
(3)若∠2+∠_______=180°,则可判断CD∥AB,因为______ ______.
______.