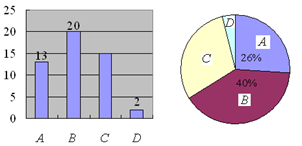
在平面直角坐标系中,抛物线与轴交于,两点(点在点左侧),与轴交于点,顶点为,对称轴与轴交于点.
(1)如图1,连接,.若点为直线上方抛物线上一动点,过点作轴交于点,作于点,过点作交轴于点.点,分别在对称轴和轴上运动,连接,.当的周长最大时,求的最小值及点的坐标.
(2)如图2,将抛物线沿射线方向平移,当抛物线经过原点时停止平移,此时抛物线顶点记为,为直线上一点,连接点,,,△能否构成等腰三角形?若能,直接写出满足条件的点的坐标;若不能,请说明理由.
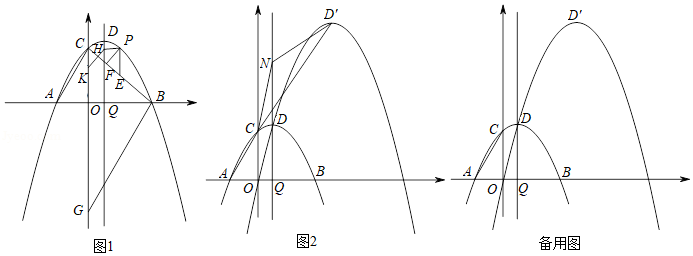
(6分) 某中学组织全体学生参加了“喜迎青奥,走出校门,服务社会”的活动.该中学以九年级(2)班为样本,统计了该班学生宣传青奥,打扫街道,去敬老院服务和在十字路口值勤的人数,并做了如下直方图和扇形统计图(A~宣传青奥;B~打扫街道;C~去敬老院服务;D~在十字路口值勤).(1)求去敬老院服务对应的扇形圆心角的度数;
(2)若该中学共有800学生,请估计这次活动中在十字路口值勤的学生共有多少人?
(6分)在直角坐标平面内,二次函数y=ax2+bx-3(a≠0)图象的顶点为A(1,-4).(1)求该二次函数关系式;
(2)将该二次函数图象向上平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与
 轴的另一个交点的坐标.
轴的另一个交点的坐标.
(6分)如图,已知,四边形ABCD为梯形,分别过点A、D作底边BC的垂线,垂足分别为点E、F.四边形ADFE是何种特殊的四边形?请写出你的理由.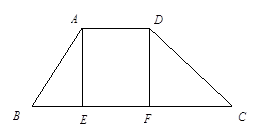
(6分)解不等式组并写出它的所有整数解.
(6分)先化简,再求值.
(-)÷,其中x=+1