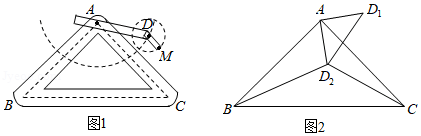
如图1是实验室中的一种摆动装置，在地面上，支架是底边为的等腰直角三角形，摆动臂可绕点旋转，摆动臂可绕点旋转，，．
（1）在旋转过程中，
①当，，三点在同一直线上时，求的长．
②当，，三点为同一直角三角形的顶点时，求的长．
（2）若摆动臂顺时针旋转，点的位置由外的点转到其内的点处，连结，如图2，此时，，求的长．
（本题10分）如图，E为正方形ABCD对角线BD上的一点，且BE＝BC＝1．
（1）求∠DCE的度数；
（2）点P在EC上，作PM⊥BD于M，PN⊥BC于N，求PM＋PN的值．
（本题9分）喝绿茶前需要烧水和泡茶两个工序，即需要将电热水壶中的水烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y（℃）与时间x（min）成一次函数关系；停止加热过了1分钟后，水壶中水的温度 y（℃）与时间x（min）近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．
（1）分别求出图中所对应的函数关系式，并且写出自变量x的取值范围；
（2）从水壶中的水烧开（100℃）降到80℃就可以进行泡制绿茶，问从水烧开到泡茶需要等待多长时间？
（本题8分）设点A的坐标（x，y），其中横坐标x可取-1，2，纵坐标y可取-1，1，2。
（1）求出点A的坐标的所有等可能结果（用树形图或列表法求解）；
（2）求点A与点B（1，-1）关于原点对称的概率。
（本题5分）为了构建城市立体道路网络，决定修建一条轻轨铁路，为了使工程提前6个月完成，需将原定的工作效率提高25%．原计划完成这项工程需要多少个月？
（本题5分）如图所示，已知BD⊥CD于D，EF⊥CD于F，
，
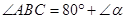，其中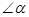
为锐角，求证：
。