已知关于的一元二次方程.
(1)求证:无论为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为、,满足,求的值;
(3)若的斜边为5,另外两条边的长恰好是方程的两个根、,求的内切圆半径.
计算: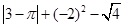
一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
| 时间 |
7:00 |
8:00 |
9:00 |
10:00 |
11:00 |
12:00 |
13:00 |
14:00 |
15:00 |
体温 (与前一次比较) (与前一次比较) |
升0.2 |
降1.0 |
降0.8 |
降1.0 |
降0.6 |
升0.4 |
降0.2 |
降0.2 |
降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
把几个数用大括号围起来,中间用逗号断开,如: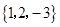 、
、 ,我们称之为集合,其中的数称其为集合的元素。如果一个集合满足:当有理数
,我们称之为集合,其中的数称其为集合的元素。如果一个集合满足:当有理数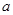 是集合的元素时,有理数6
是集合的元素时,有理数6 也必是这个集合的元素,这样的集合我们称为好的集合。
也必是这个集合的元素,这样的集合我们称为好的集合。
(1)请你判断集合 ,
, 是不是好的集合?
是不是好的集合?
(2)请你写出满足条件的两个好的集合的例子。
有这样一道计算题:
计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=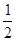 ,y=-1。甲同学把x=
,y=-1。甲同学把x=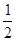 错看成x=-
错看成x=-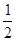 ,但计算结果仍正确,你说是怎么一回事?
,但计算结果仍正确,你说是怎么一回事?
已知: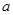 、
、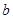 互为相反数,
互为相反数,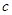 、
、 互为倒数,
互为倒数, 的绝对值是最小的正整数,
的绝对值是最小的正整数,
求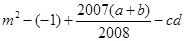 的值。
的值。