如图,线段经过的圆心,交于、两点,,为的弦,连结,,连结并延长交于点,连结交于点.
(1)求证:直线是的切线;
(2)求的半径的长;
(3)求线段的长.

如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: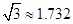 )
)
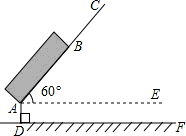
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,求DE∶EC的值.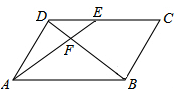
如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。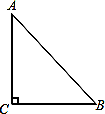
已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长