某校举行了自贡市创建全国文明城市知识竞赛活动,初一年级全体同学参加了知识竞赛.
收集教据:现随机抽取了初一年级30名同学的“创文知识竞赛”成绩,分数如下(单位:分)
90 85 68 92 81 84 95 93 87 89 78 99 89 85 97
88 81 95 86 98 95 93 89 86 84 87 79 85 89 82
整理分析数据:
成绩(单位:分) |
频数(人数) |
1 |
|
2 |
|
17 |
|
|

(1)请将图表中空缺的部分补充完整;
(2)学校决定表彰“创文知识竞赛”成绩在90分及其以上的同学.根据上面统计结果估计该校初一年级360人中,约有多少人将获得表彰;
(3)“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .
化简求值:: ,其中
,其中
化简(6分)
(1) .
.
(2)
一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)观察表中数据规律填表:
(2)一家酒楼,按上图的方式拼桌,要使拼 成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来就餐,哪种拼桌的方式更好?最少要用多少张餐桌?
如图,有一个几何体,请画出从不同方向看它的平面图形(6分)
(1)从正面看:
(2)从左面看
(3)从上面看
想一想(每空1分,共5分):
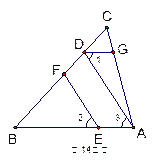
如图(EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.因为EF∥AD,所以∠2=___.又因为∠1=∠2,所以∠1=∠3.所以AB∥__.所以∠BAC+__=180°.因为∠BAC=70°,所以∠AGD=____.