如图,在正方形 中, 、 分别是 、 上的点,且 , 、 分别交 于 、 ,连接 、 ,有以下结论:
①
②当 时,
③
④存在点 、 ,使得
其中正确的个数是

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
下列性质中是矩形和菱形共有的性质是( ).
| A.相邻两角都互补 | B.相邻两边都相等 |
| C.对角线是对称轴 | D.对角线垂直且相等 |
如图,矩形的长和宽分别为8cm和4cm,截去一个宽为x的小矩形(阴影部分)后余下另一个矩形的面积S与x之间的关系可表示为( ).
| A.S=4x | B.S=4(8-x) | C.S=8(4-x) | D.S=8x |
如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的关系是( )
A、S1+S3=S2 B、2S1+S3=S2 C、2S3-S2=S1 D、4S1-S3=S2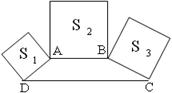
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )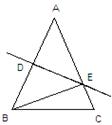
| A.12cm | B.10cm | C.8cm | D.6cm |
若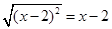 ,则
,则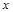 的取值范围是()
的取值范围是()
A.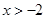 |
B.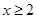 |
C.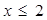 且 且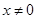 |
D.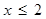 |