为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级,随机抽取该校部分学生的征文比赛成绩进行分析,并绘制了如下的统计图表:
| 成绩等级 |
A |
B |
C |
D |
| 人数 |
60 |
x |
y |
10 |
| 占抽查学生总数的百分比 |
30% |
50% |
15% |
m |
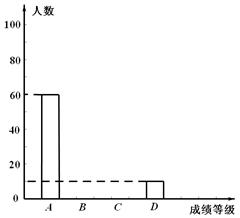
根据表中的信息,解决下列问题:
(1)本次抽查的学生共有 ▲名;
(2)表中x、y和m所表示的数分别为x= ▲,y= ▲,m= ▲;
(3)补全条形统计图。
解方程组和不等式组:
(1)解方程组: ;(2)解不等式组:
;(2)解不等式组: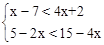 。
。
化简(1)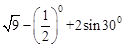 ; (2)
; (2) 。
。
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线
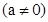 过点A。
过点A。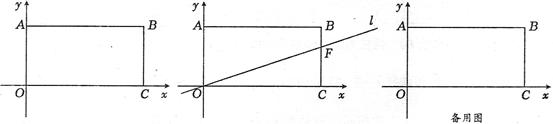
(1)(2分)求c的值;.
(2)(6分)若a=-l,且抛物线与矩形有且只有三个交点A、D、E,求△ADE的面积S的最大值;
(3)(6分)若抛物线与矩形有且只有三个交点A、M、N,线段MN的垂直平分线l过点O,交线段BC于点
F。当BF=1时,求抛物线的解析式.
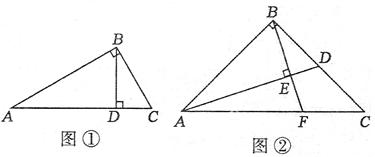
(1)(3分)如图①,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.
求证:AB2=AD·AC;
(2)(4分)如图②,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC
于点F.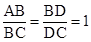 ,求
,求 的值;
的值;
(3)(5分) 在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD
于点E,交直线AC于点F。若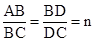 ,请探究并直接写出
,请探究并直接写出 的所有可能的值(用含n的式子表
的所有可能的值(用含n的式子表
示),不必证明.