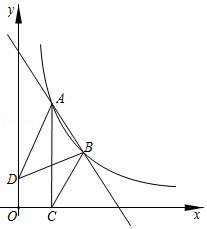
如图,点,,是直线与反比例函数图象的两个交点,轴,垂足为点,已知,连接,,.
(1)求直线的表达式;
(2)和的面积分别为,.求.
(本题6分)如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整。(请画出三种)
(本题6分)解下列不等式组,并把解集表示在数轴上
(2)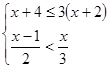
(本小题12分)自温家宝在北京某学校调研以来,教师的工资受到了不同程度的影响,为了落实“调动教师积极性、不低于公务员人均水平”政策,某县政府2010年1月份开始调整了教师的月工资分配方案:调整后月工资由基本保障工资和绩效工资两部分组成(绩效工 资=每课的课时系数×课时总数).若月基本工资为2540元,下表是甲、乙两位教师今年1月份的工资情况信息:
资=每课的课时系数×课时总数).若月基本工资为2540元,下表是甲、乙两位教师今年1月份的工资情况信息:
| 教师 |
甲 |
乙 |
| 月课时总数 |
220 |
|
| 月工资(元) |
3860 |
4340 |
(1)求工资分配方案调整后,每课的课时系数和乙教师的月课时总数。
(2)《中华人民共和国个人所得税法》规定,公民全月工资,其中2000元不必纳税,超过2000元的部分为全月应纳税所得额;全月应纳税所得额不超过500元的部分税率为5%,全月应纳税所得额超过500元至2000元的部分税率为10%,全月应纳税所得额超过2000元至5000元部分税率为15%……[例如乙教师的全月应纳税所得额是4340-2000=2340元,每月所缴个人所得税计算为500*5%+(2000-500)*10%+(2340-2000)*15%=226元)]
①请你帮忙计算甲教师的每月个人所得税;
②已知丙教师每月缴税220元,求缴税后的月工资为多少?
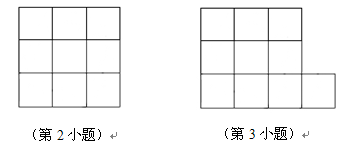
(本小题12分)如图,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开后拼成一个大正方形。
拼成的大正方形的面积与边长分别是多少?
你能在下图3×3方格中,连接四个格点,组成面积为5的正方形吗?
你还能把十个小正方形组成的图形纸,剪开并拼成更大的正方形吗?若能,请在下图中画出图形,并求出它的边长是多少?
(本小题10分)我 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
| 题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 答错人数 |
9 |
10 |
6 |
6 |
18 |
23 |
已知这n人中,平均每题有12人答错,同时第6题答错的人数恰好是第5题答错人数的2倍,且第2题有80%的同学答对。解答下面的问题:(1)总共统计了多少人?
(2)
 第5,6两题各有多少人答错?
第5,6两题各有多少人答错?(3)将统计图
 补充完整。
补充完整。