在平面直角坐标系中，直线yx2与x轴交于点A，与y轴交于点B-优题课

游客

题文

在平面直角坐标系中，直线 $y = x + 2$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = a x^{2} + bx + c (a < 0)$ 经过点 $A$ 、 $B$ ．

（1）求 $a$ 、 $b$ 满足的关系式及 $c$ 的值．

（2）当 $x < 0$ 时，若 $y = a x^{2} + bx + c (a < 0)$ 的函数值随 $x$ 的增大而增大，求 $a$ 的取值范围．

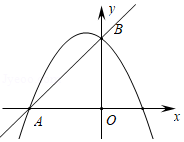
（3）如图，当 $a = - 1$ 时，在抛物线上是否存在点 $P$ ，使 $ΔPAB$ 的面积为1？若存在，请求出符合条件的所有点 $P$ 的坐标；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数的性质二次函数综合题

登录免费查看答案和解析

相关试题

计算或化简：（本小题6分）

解下列方程（每题5分，共10分）
（1）
（2）（用配方法解）

如图①②，在平面直角坐标系中，边长为2的等边△CDE恰好与坐标系中的△OAB重合，现将△CDE绕边AB的中点G(G点也是DE的中点)，按顺时针方向旋转180°到△C1DE的位置．

(1)求C1点的坐标；
(2)求经过三点O、A、C1的抛物线的解析式；
(3)如图③，⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴相交于点F，求切线BF
的解析式；
(4)抛物线上是否存在一点M，使得．若存在，请求出点M的坐标；
若不存在，请说明理由．

(1)计算:如图①,直径为的三等圆⊙O、⊙O、⊙O两两外切，切点分别为A、B、C ，求OA的长（用含的代数式表示）.

（2）探索:若干个直径为的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放，探索并求出这两种方案中层圆圈的高度和（用含、的代数式表示）.
（3）应用:现有长方体集装箱，其内空长为5米，宽为3.1米，高为3.1米.用这样的集装箱装运长为5米，底面直径（横截面的外圆直径）为0.1米的圆柱形钢管，你认为采用（2）中的哪种方案在该集装箱中装运钢管数最多？并求出一个这样的集装箱最多能装运多少根钢管？（≈1.73）

某批发市场批发甲、乙两种水果，甲种水果的销售利润（万元）与进货量（吨）近似满足函数关系；乙种水果的销售利润（万元）与进货量（吨）近似满足函数关系（其中为常数），当为1吨时，为1.4万元；当为2吨时，为2.6万元．
（1）求出的值，并写出（万元）与（吨）之间的函数关系式．
（2）如果市场准备进甲、乙两种水果共10吨，设乙种水果的进货量为吨，请你写出这两种水果所获得的销售利润之和（万元）与（吨）之间的函数关系式，并写出的取值范围。
（3）在（2）的前提下，这两种水果各进多少吨时，获得的销售利润之和最大，最大利润是多少？

试卷网试题网古诗词网作文网范文网