某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量（件与销售单价（元之间满足一次函数关系，其图象如图所示．
（1）求该商品每天的销售量与销售单价之间的函数关系式；
（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润（元最大？最大利润是多少？
（3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？
化简：（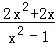
﹣
）÷ 
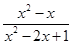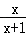，并解答：
（1）当x=3时，求原式的值；
（2）原式的值能等于﹣1吗？为什么？
请认真观察图形，解答下列问题：
（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；
（2）由（1），你能得到怎样的等量关系？请用等式表示；
（3）如果图中的a，b（a＞b）满足a2+b2=53，ab=14，求：①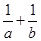
的值；②a﹣b的值．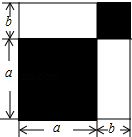
如图，△ABC中，AB=AC，∠A=40°．
（1）作边AB的垂直平分线MN（保留作图痕迹，不写作法）；
（2）在已作的图中，若MN交AC于点D，连结BD，求∠DBC的度数。
如图，∠BAC=∠DAE，∠ABD=∠ACE，AB=AC．求证：BD=CE．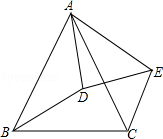
先化简，再求值：
（x﹣1）（x﹣2）﹣3x（x+3）+2（x+2）（x﹣1），其中x=-1。