如图,在矩形中,,,点在上,将沿折叠,点恰好落在对角线上的点,为上一点,经过点,
(1)求证:是的切线;
(2)在边上截取,点是线段的黄金分割点吗?请说明理由.

九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
⑴有多少种购买方案?请列举所有可能的结果;
⑵从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
某小区前坪有一块空地,现想建成一块面积大于48平方米,周长小于34米的矩形绿化草地,已知一边长为8米,设其邻边长为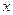 米,求
米,求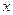 的整数解.
的整数解.
2011年我市体卫站对某校九年级学生体育测试情况进行调研,从该校360名九年级学生中抽取了部分学生的成绩(成绩分为A、B、C三个层 次)进行分析,绘制了频数分布表与频数分布直方图(如图),请根据图表信息解答下列问题:
次)进行分析,绘制了频数分布表与频数分布直方图(如图),请根据图表信息解答下列问题:
⑴补全频数分布表与频数分布直方图;
⑵如果成绩为A等级的同学属于优秀,请你估计该校九年级约有多少人达到优秀水平?

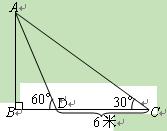
莲城中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).
⑴AD=_______米;
⑵求旗杆AB的高度( ).
).
我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
||
| 每 辆 汽 车 运 载 量 |
(吨) |
A型 |
 2 2 |
2 |
|
| B型 |
4 |
2 |
|||
| C型 |
1 |
6 |
|||
| 车型 |
A |
B |
C |
| 每辆车运费(元) |
1500 |
1800 |
2000 |
(1)设A型汽车安排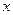 辆,B 型汽车安排
辆,B 型汽车安排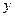 辆,求
辆,求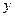 与
与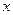 之间的函数关系式。
之间的函数关系式。
(2)如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3)为节约运费,应采用(2)中哪种方案?并求出最少运费。