如图，顶点为M的抛物线yax2bx3与x轴交于A(3,0)，-优题课

游客

题文

如图，顶点为 $M$ 的抛物线 $y = a x^{2} + bx + 3$ 与 $x$ 轴交于 $A (3, 0)$ ， $B (- 1, 0)$ 两点，与 $y$ 轴交于点 $C$ ．

（1）求这条抛物线对应的函数表达式；

（2）问在 $y$ 轴上是否存在一点 $P$ ，使得 $ΔPAM$ 为直角三角形？若存在，求出点 $P$ 的坐标；若不存在，说明理由．

（3）若在第一象限的抛物线下方有一动点 $D$ ，满足 $DA = OA$ ，过 $D$ 作 $DG ⊥ x$ 轴于点 $G$ ，设 $ΔADG$ 的内心为 $I$ ，试求 $CI$ 的最小值．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式点与圆的位置关系二次函数综合题切线长定理三角形的内切圆与内心

登录免费查看答案和解析

相关试题

如图所示，已知E为 ABCD的边CD延长线上的一点，连接BE交AC于O，交AD于F．

求证：（1）△ABO∽△CEO
（2）BO²＝OF•OE．

小明和小华在如图所示的两个转盘上玩一个游戏．两个转盘中指针落在每一个数字上的机会都均等，现同时自由转动甲、乙两个转盘，转盘停止后，指针各指向一个数字，若指针停在等分线上，则重转一次，直至指针指向某一数字为止．用所指的两个数字作乘积．如果积为奇数，则小明赢；如果积为偶数，则小华赢，这个游戏公平吗？请利用树状图或表格说明理由。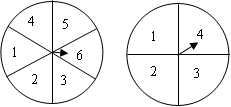

如图，AB和DE是直立在地面上的两根立柱.AB="5" m，某一时刻AB在阳光下的投影BC=3m.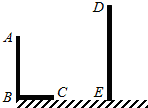

（1）请你在图中画出此时DE在阳光下的投影EF；
（2）在测量AB的投影时，同时测量出DE 在阳光下的投影长为6m，请你计算DE 的长.

如图，在△ABC中，∠B=90°，AB=6，BC=8．点P从点A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动．设P、Q分别从A、B同时出发，运动时间为t，当其中一点先到达终点时，另一点也停止运动．解答下列问题：

（1）经过几秒，△PBQ的面积等于8cm²？
（2）是否存在这样的时刻t，使线段PQ恰好平分△ABC的面积？若存在，求出运动时间t；若不存在，请说明理由．

如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C。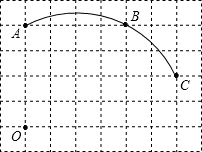

⑴请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，作出该圆弧所在圆的圆心D，并连接AD、CD。
⑵请在⑴的基础上，完成下列填空：
①写出点的坐标： C_______、D_______；
②直接写出⊙D半径＝_______（结果保留根号）；
③直接写出∠ADC＝_______；
④若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面的半径．

试卷网试题网古诗词网作文网范文网