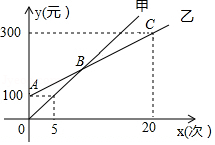
某生态体验园推出了甲、乙两种消费卡,设入园次数为时所需费用为元,选择这两种卡消费时,与的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,关于的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
(1)解不等式 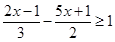 ,并把它的解集在数轴上表示出来
,并把它的解集在数轴上表示出来
(2)解不等式组 ,并在数轴上表示解集。
,并在数轴上表示解集。
解方程组:
(1)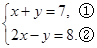
(2)
如果一条抛物线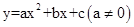 与
与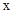 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是三角形;
(2)如图,△OAB是抛物线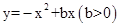 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.
边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1),现将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中, AB边交DF于点M,BC边交DG于点N.
(1)求边DA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时(如图2),求正方形ABCD旋转的度数;
(3)如图3,设△MBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?请证明你的结论.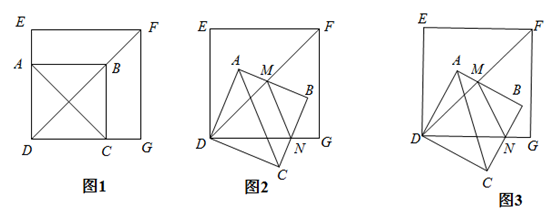
已知关于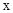 的一元二次方程
的一元二次方程 有实数根,
有实数根,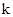 为正整数.
为正整数.
(1)求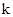 的值;
的值;
(2)当此方程有两个不为0的整数根时,将关于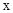 的二次函数
的二次函数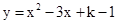 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于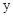 轴左侧的部分沿
轴左侧的部分沿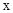 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出 的取值范围.
的取值范围.