如图,二次函数的图象过原点,与轴的另一个交点为
(1)求该二次函数的解析式;
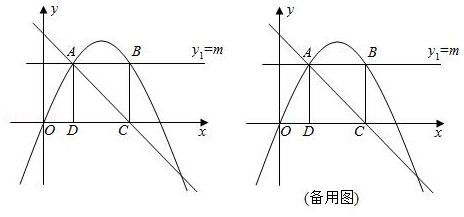
(2)在轴上方作轴的平行线,交二次函数图象于、两点,过、两点分别作轴的垂线,垂足分别为点、点.当矩形为正方形时,求的值;
(3)在(2)的条件下,动点从点出发沿射线以每秒1个单位长度匀速运动,同时动点以相同的速度从点出发沿线段匀速运动,到达点时立即原速返回,当动点返回到点时,、两点同时停止运动,设运动时间为秒.过点向轴作垂线,交抛物线于点,交直线于点,问:以、、、四点为顶点构成的四边形能否是平行四边形.若能,请求出的值;若不能,请说明理由.
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上

( 1 )将 向左平移 个单位得到 ,并写出点 的坐标;
( 2 )画出 绕点 顺时针旋转 后得到的 ,并写出点 的坐标;
( 3 )在( 2 )的条件下,求 在旋转过程中扫过的面积(结果保留 ).
发现规律:
( 1 )如图①, 与 都是等边三角形,直线 交于点 .直线 , 交于点 .求 的度数
( 2 )已知: 与 的位置如图②所示,直线 交于点 .直线 , 交于点 .若 , ,求 的度数
应用结论:
( 3 )如图③,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 , 为 轴上一动点,连接 .将线段 绕点 逆时针旋转 得到线段 ,连接 , ,求线段 长度的最小值


已知,在平面直角坐标系中,抛物线 的顶点为 ,点 的坐标为
( 1 )求抛物线过点 时顶点 的坐标
( 2 )点 的坐标记为 ,求 与 的函数表达式;
( 3 )已知 点的坐标为 ,当 取何值时,抛物线 与线段 只有一个交点

小伟和小梅两位同学玩掷骰子的游戏,两人各掷一次均匀的骰子,以掷出的点数之差的绝对值判断输赢.若所得数值等于 , , ,则小伟胜:若所得数值等于 , , ,则小梅胜
( 1 )请利用表格分别求出小伟、小梅获胜的概率

( 2 )判断上述游戏是否公平.如果公平,请说明理由;如果不公平,请利用上表修改游戏规则,以确保游戏的公平性
如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点
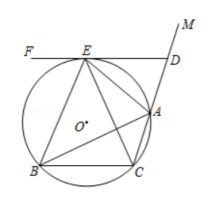
求证:( 1 ) ;
( 2 ) 为 的切线.