如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1,P2交 OA于M,交OB于N,若P1P2=6,则△PMN的周长为()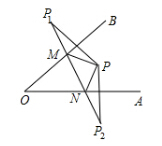
A.4 B.5 C.6 D.7
如果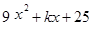 是一个完全平方式,那么k的值是()
是一个完全平方式,那么k的值是()
| A.30 | B.±30 | C.15 | D.±15 |
多项式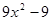 因式分解的结果是()
因式分解的结果是()
A.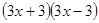 |
B.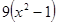 |
C.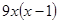 |
D.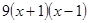 |
如图,AD是△ABC的角平分线,从点D向AB、AC两边作垂线段,垂足分别为E、F,那么下列结论中错误的是()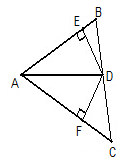
A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF
如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在 ()
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边垂直平分线的交点处