某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为、、、、,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 |
频率 |
0.35 |
|
0.20 |
|
0.05 |
(1)求本次调查的小型汽车数量及,的值;
(2)补全频数分布直方图;
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.

如图,Rt△ABC中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,OG⊥BC于G点.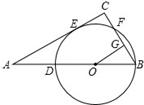
(1)求证:CE=OG;
(2)若BC=3cm,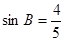 ,求线段AD的长.
,求线段AD的长.
甲、乙两人在相同的条件下各射靶5次,每次射靶的成绩情况如图所示.
(1)请你根据图中的数据填写下表:
| 姓名 |
平均数(环) |
众数(环) |
方差 |
| 甲 |
7 |
||
| 乙 |
6 |
2.8 |
(2)从平均数和方差相结合看,分析谁的成绩好些.
解方程:(1) ;(2)
;(2)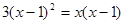 .
.
计算:(1) ;(2)2sin60°-3tan30°+
;(2)2sin60°-3tan30°+ -(-1)2012.
-(-1)2012.
如图,已知 中,∠B=∠C,
中,∠B=∠C, 厘米,
厘米,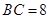 厘米,点
厘米,点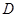 为
为 的中点.
的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使 与
与 全等?
全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿 三边运动,则经过秒时点P与点Q第一次在
三边运动,则经过秒时点P与点Q第一次在 的其中一条边上相遇.
的其中一条边上相遇.